【導(dǎo)讀】電阻(R)、電感器(L)和電容器(C)是電子學(xué)的三個基本無源元件。它們的特性和行為已經(jīng)在交流電阻、交流電感和交流電容中詳細(xì)介紹過教程本文將重點(diǎn)討論這三個元件的串聯(lián)組合,稱為串聯(lián)RLC電路。首先,介紹了三種本構(gòu)元件的交流特性,并簡要介紹了RLC電路。
串聯(lián)RLC電路
演示
RLC電路的表示如下圖1所示:
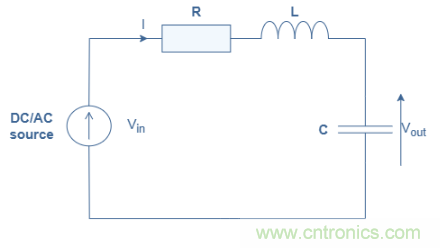
圖1:RLC系列電路示意圖
電阻器是一個純電阻元件,在其上的電壓和電流之間沒有相移。其阻抗(ZR)在直流和交流區(qū)保持不變,等于R(單位:Ω),電感是一個純無功元件,相移為+90°或+π/2rad。其阻抗由ZL=jωL給出,ω是交流情況下電壓/電流的角頻率,L是電感(單位:H)。在直流區(qū),電感器表現(xiàn)為兩個端子之間的短路;在交流區(qū),電感器的阻抗隨著頻率。電感器通常被認(rèn)為是一種元件,它可以抵抗電流。電容器也是純無功元件,但其相移為-90°或-π/2rad。它的阻抗由ZC=-j/Cω給出,C是電容(單位為F),因此當(dāng)頻率增加時,它在直流區(qū)表現(xiàn)為開路,在交流區(qū)表現(xiàn)為短路電壓輸入圖1,這三個組件串聯(lián)在一起。電路由直流或交流電源供電,輸出是電容器上的電壓。前面的阻抗之和是電路阻抗的總和說明:ZRLC=ZR+ZL+ZC=R+j(Lω-(1/Cω))在下一節(jié)中,我們將介紹該電路對電壓階躍(也稱為瞬態(tài)響應(yīng))的響應(yīng)。
瞬態(tài)響應(yīng)
在本節(jié)中,我們將重點(diǎn)關(guān)注圖1中所示電路的行為,當(dāng)對其應(yīng)用重邊步驟H(t)時:
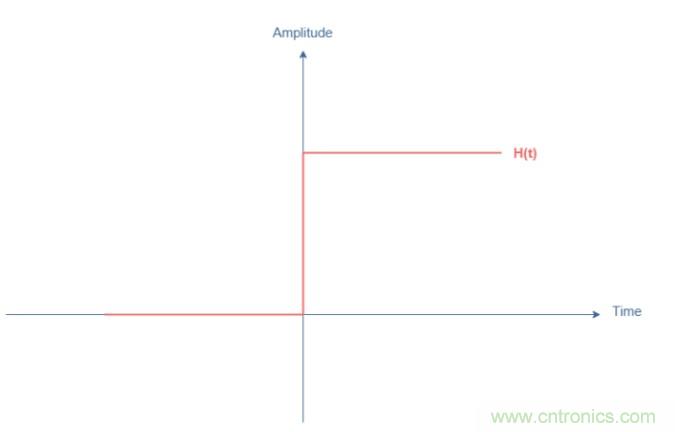
圖2:Heaviside函數(shù)說明
升程階躍的特征是t<0等于0,t>0時等于Vin。這兩種狀態(tài)之間的轉(zhuǎn)換類似于脈沖,因為當(dāng)t=0時,導(dǎo)數(shù)趨于+∞。通過對電路進(jìn)行網(wǎng)絡(luò)分析,我們可以得出:Vin=R×I+L×dI/dt+Vout。此外,我們知道電流可以改寫為I=C×dVout/dt,由此得到以下二階微分方程:
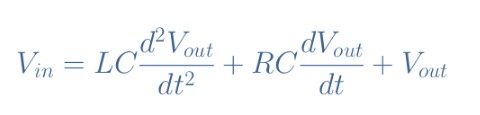
式1:串聯(lián)RLC電路的二階微分方程
這種方程的解是永久響應(yīng)(時間常數(shù))和瞬態(tài)響應(yīng)Vout,tr(時間變量)的總和。永久響應(yīng)的求解是一個方程1的永久解,其瞬態(tài)響應(yīng)很復(fù)雜,涉及許多步驟,本文不詳細(xì)介紹。我們承認(rèn)它的表達(dá)式可以有三種不同的形式,取決于Q=(1/R)√(L/C)的值,稱為電路的品質(zhì)因數(shù)。另一個重要參數(shù)是ω0=1/√(LC),這是電路。何時Q> 1/2,該系統(tǒng)被稱為偽周期響應(yīng)或欠阻尼響應(yīng),瞬態(tài)響應(yīng)可采用Vout、tr=Ae-αtcos(ωt+Φ)的形式寫入??紤]電路初始條件(如果電容器充電或未充電…)可以找到常數(shù)A、α和Φ。脈動ω稱為角頻率,取決于基本頻率ω0。當(dāng)Q<1/2時,該系統(tǒng)被稱為非周期或過采樣響應(yīng),瞬態(tài)響應(yīng)形式為Vout,tr=e-αt(A1e-ωt+A2eωt),最后一種情況是Q=1/2,對應(yīng)于臨界狀態(tài)或臨界阻尼響應(yīng)。在這種情況下,Vout,tr=(A+Bt)e-ω0t,Vin:
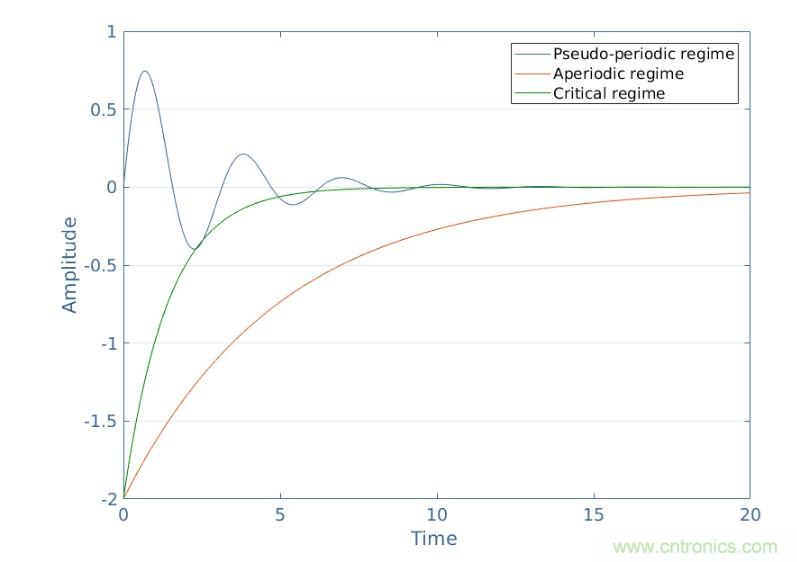
圖3:瞬態(tài)響應(yīng)的不同區(qū)域曲線
當(dāng)時間增加時,每條曲線趨于0。這是有意義的,因為我們知道Vout=Vin+Vout,tr和Vout(t→+∞)=Vin,因此,Vout,tr→0。但是,不同的可能瞬態(tài)響應(yīng)在相同的速度和行為下不趨向于0。臨界狀態(tài)是最快趨于0的狀態(tài),而非周期狀態(tài)是最慢的。偽周期區(qū)域呈現(xiàn)振幅減小的振蕩指數(shù)級的。為了一個未知的RLC電路,用最佳可能曲線識別和匹配瞬態(tài)響應(yīng),可以得到電路的重要特性,如ω0和Q。
交流響應(yīng)
在本節(jié)中,我們考慮圖1中所示的同一電路,現(xiàn)在使用交流電源供電。利用復(fù)符號dX/dt=jωX的性質(zhì),ω是源的角頻率,我們可以用以下形式重寫方程1:
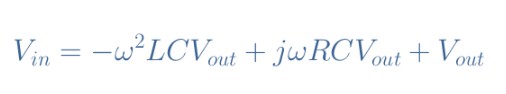
式2:串聯(lián)RLC電路的復(fù)二階微分方程
然后我們可以表示Vout/Vin的比值,這是串聯(lián)RLC電路的傳遞函數(shù)T:
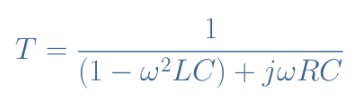
公式3:串聯(lián)RLC電路的傳遞函數(shù)
知道Q=(1/R)√(L/C),ω0=1/√(LC),并考慮參數(shù)x=ω/ω0,稱為歸一化頻率,我們可以重新整理方程3,寫出傳遞函數(shù)的標(biāo)準(zhǔn)形式,從而簡化并使表達(dá)式更緊湊:
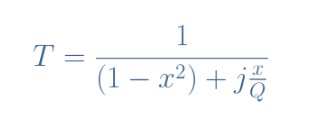
公式4:RLC電路傳遞函數(shù)的標(biāo)準(zhǔn)形式
為了獲得作為參數(shù)x的函數(shù)的電路增益,繪制傳遞函數(shù)的范數(shù)是很有趣的。本例中取了R=10Ω和20Ω,L=0.2 H,C=100μF的值:
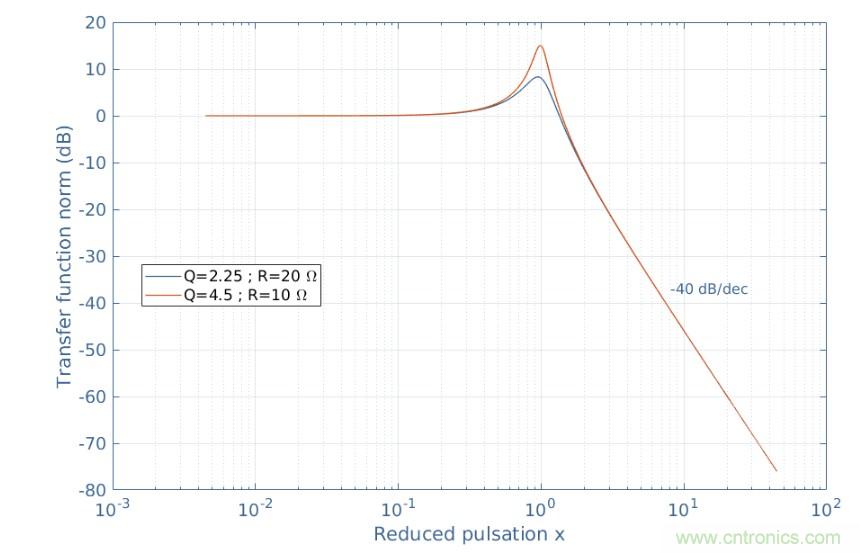
圖4:串聯(lián)RLC電路的增益
我們可以注意到,圖1中所示的串聯(lián)RLC電路在交流區(qū)起到了二階低通濾波器的作用,因為它降低了高于ω0的脈動的輸出信號,通常稱為電路。二階濾波器具有對ω0附近頻率的信號進(jìn)行輕微放大的特性,并且在截止頻率之后呈現(xiàn)-40 dB/dec的降低,而不是僅-20 dB/dec,例如一階過濾器。它在圖4中強(qiáng)調(diào)了Q值(取決于R)對曲線形狀的影響。共振頻率附近的峰值確實(shí)以其帶寬Δω=ω0/Q為特征。在本例中,ω0=223 rad/s和Q=4.5或2.25,這使得橙色曲線的Δω=50 rad/s較窄,藍(lán)色曲線的帶寬為100 rad/s。因此,我們可以注意到,品質(zhì)因數(shù)決定了共振是窄的(大Q)還是寬的(小Q)。如前一節(jié)所述,用最佳可能曲線擬合未知電路的傳遞函數(shù),可以了解電路的特性,從而確定其組成元件的值。
RCL和CLR配置
基本元件R、L和C的其它組合可以提供不同類型的濾波器。我們之前已經(jīng)看到RLC配置是二階低通濾波器,但是如果我們在它們之間切換一些組件呢?圖5和圖6顯示了兩種新的配置,即RCL和CLR電路:
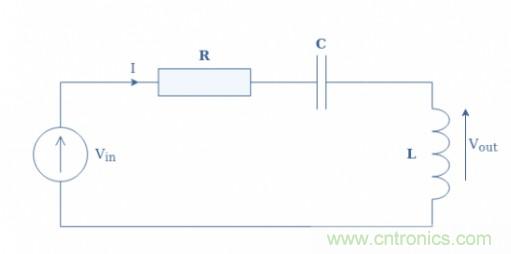
圖5:RCL電路示意圖
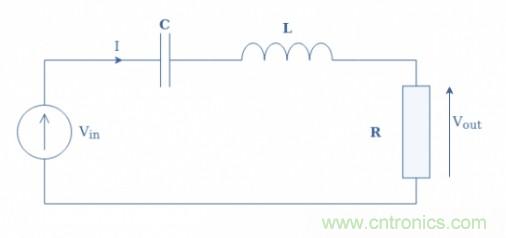
圖6:CLR電路示意圖
盡管這些電路和圖1中所示的原始RLC電路之間的變化很小,交流響應(yīng)非常大不一樣。它可以證明這兩個電路的傳遞函數(shù)由等式4和5給出:
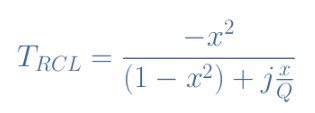
公式5:RCL電路傳遞函數(shù)
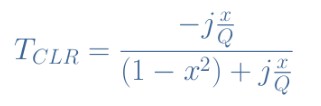
公式6:CLR電路傳遞函數(shù)
通過繪制具有相同值的傳遞函數(shù)范數(shù):R=10Ω和20Ω,L=0.2h,C=100μF,揭示了這些新濾波器的性質(zhì)。
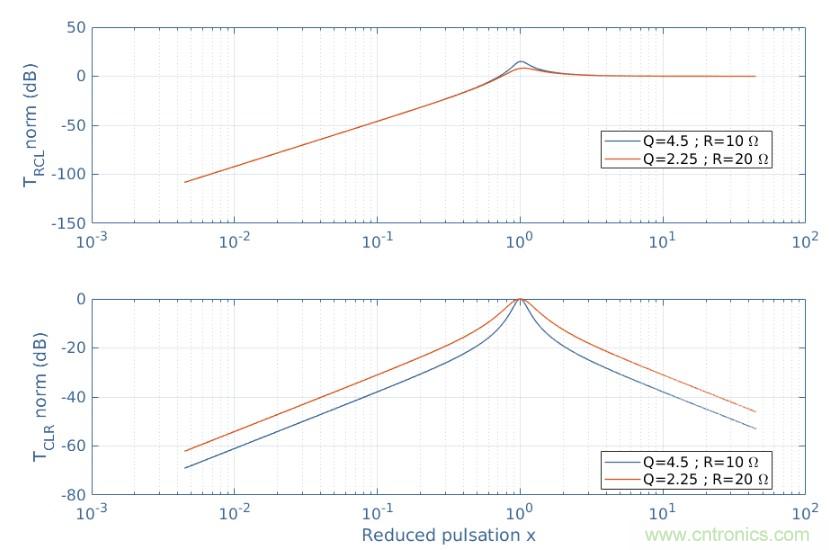
圖7:串聯(lián)RCL和CLR電路的增益
RCL電路是一種二階高通濾波器,因為它可以衰減ω0以下的頻率。電路CLR是一個帶通濾波器,因為它只放大ω0左右的頻率。請注意,與上一節(jié)中關(guān)于曲線形狀作為Q函數(shù)的注釋仍然適用于這兩個過濾器。
結(jié)論
串聯(lián)RLC電路是由三個基本電子元件串聯(lián)而成:電阻器、電感器和電容器。電阻的阻抗是實(shí)數(shù),電感器和電容器的阻抗是純虛數(shù),電路的總阻抗是這三個阻抗之和,因此是一個復(fù)數(shù)數(shù)字。那個第二節(jié)首先定義并給出電路的瞬態(tài)響應(yīng)。它包括在高電壓階躍下研究電路的行為。通過研究與電路相關(guān)的二階微分方程的可能解,可能存在三種情況:
欠阻尼響應(yīng),信號向永久值Vin緩慢振蕩。
信號緩慢增加到永久值的過阻尼響應(yīng)。
臨界阻尼響應(yīng)是信號向永久值增長最快的情況。
第三部分介紹了電路的交流響應(yīng)。當(dāng)提供交流信號時,微分方程可以寫成復(fù)數(shù)形式,以便找到電路的傳遞函數(shù)。繪制該函數(shù)的范數(shù)表明串聯(lián)RLC電路具有二階低通特性過濾器。輸入最后一節(jié)研究了RCL和CLR兩種不同的結(jié)構(gòu)。這一節(jié)說明,二階高通濾波器或帶通濾波器可以由同一電路通過簡單的開關(guān)元件來實(shí)現(xiàn)。
推薦閱讀:





