【導讀】噪聲的重要特性之一就是其頻譜密度。電壓噪聲頻譜密度是指每平方根赫茲的有效( RMS) 噪聲電壓(通常單位為nV/rt-Hz)。功率譜密度的單位為W/Hz。在上一篇文章中,我們了解到電阻的熱噪聲可用方程式 2.1 計算得出。
噪聲的重要特性之一就是其頻譜密度。電壓噪聲頻譜密度是指每平方根赫茲的有效( RMS) 噪聲電壓(通常單位為nV/rt-Hz)。功率譜密度的單位為W/Hz。在上一篇文章中,我們了解到電阻的熱噪聲可用方程式 2.1 計算得出。該算式經(jīng)過修改也可適用于頻譜密度。熱噪聲的重要特性之一就在于頻譜密度圖較平坦(也就是說所有頻率的能量相同)。因此,熱噪聲有時也稱作寬帶噪聲。運算放大器也存在寬帶噪聲。寬帶噪聲即為頻譜密度圖較平坦的噪聲。
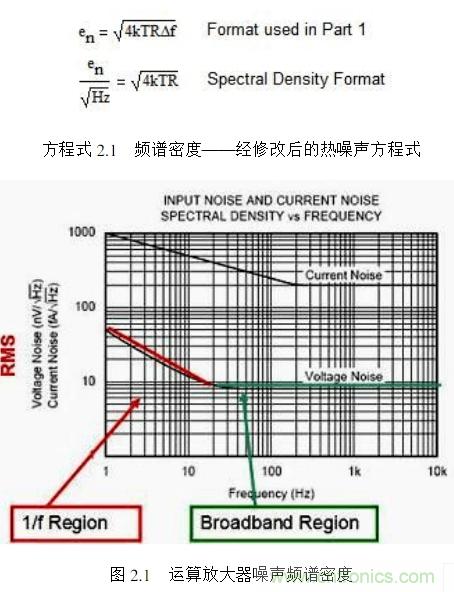
運算放大器的噪聲模型與頻譜密度曲線
除了寬帶噪聲之外,運算放大器常還有低頻噪聲區(qū),該區(qū)的頻譜密度圖并不平坦。這種噪聲稱作 1/f 噪聲,或閃爍噪聲,或低頻噪聲。通常說來,1/f 噪聲的功率譜以 1/f 的速率下降。這就是說,電壓譜會以 1/f(1/2 ) 的速率下降。不過實際上,1/f 函數(shù)的指數(shù)會略有偏差。圖 2.1 顯示了典型運算放大器在 1/f 區(qū)及寬帶區(qū)的頻譜情況。請注意,頻譜密度圖還顯示了電流噪聲情況(單位為 fA/rt-Hz)。
我們還應注意到另一點重要的情況,即 1/f 噪聲還能用正態(tài)分布曲線表示,因此 部分中介紹的數(shù)學原理仍然適用。圖 2.2 顯示了1/f 噪聲的時域情況。請注意,本圖的 X 軸單位為秒,隨時間發(fā)生較慢變化是1/f 噪聲的典型特征。
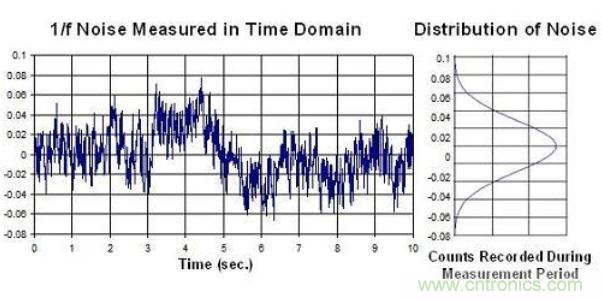
圖 2.2:時域所對應的 1/f 噪聲及統(tǒng)計學分析結(jié)果
圖 2.3 描述了運算放大器噪聲的標準模型,其包括兩個不相關的電流噪聲源與一個電壓噪聲源,連接于運算放大器的輸入端。我們可將電壓噪聲源視為隨時間變化的輸入偏移電壓分量,而電流噪聲源則可視為隨時間變化的偏置電流分量。
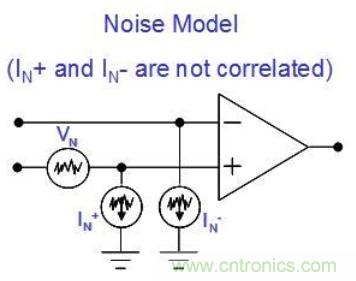
圖 2.3:運算放大器的噪聲模型
運算放大器噪聲分析方法
運算放大器噪聲分析方法是根據(jù)運放數(shù)據(jù)表上的數(shù)據(jù)計算出運放電路峰峰值輸出噪聲。在介紹有關方法的時候,我們所用的算式適用于 簡單的運算放大器電路。就更復雜的電路而言,這些算式也有助于我們大致了解可預見的噪聲輸出情況。我們也可針對這些更復雜的電路提供較準確的計算公式,但其中涉及的數(shù)學計算將更為復雜。對更復雜的電路而言,或許我們 應采用三步走的辦法。首先,用算式進行粗略的估算;然后,采用 spice 仿真程序進行更準確的估算; 通過測量來確認結(jié)果。
我們將以 TI OPA277 的簡單非反向放大器為例來說明有關電路的情況(見圖 2.4)。我們的目標是測定峰峰值輸出噪聲。為了實現(xiàn)這一目的,我們應考慮運算放大器的電流噪聲、電壓噪聲以及電阻熱噪聲。我們將根據(jù)產(chǎn)品說明書中的頻譜密度曲線來確定上述噪聲源的大小。此外,我們還要考慮電路增益與帶寬問題。
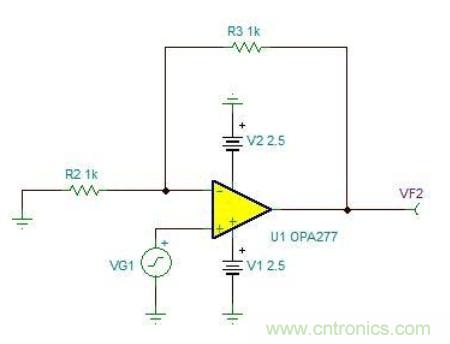
圖 2.4:噪聲分析電路示例
首先,我們應了解如何將噪聲頻譜密度曲線轉(zhuǎn)換為噪聲源。為了實現(xiàn)這一目的,我們需進行微積分運算。簡單提醒一句,積分函數(shù)確定曲線下方的面積。圖 2.5 顯示,我們只須將長寬相乘(即矩形區(qū)域面積),便能獲得常數(shù)函數(shù)的積分。這種轉(zhuǎn)換頻譜密度曲線為噪聲源的關系比較簡單。
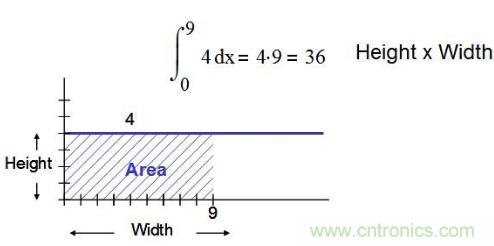
圖 2.5:通過積分計算曲線下方面積
人們通常會說,只有將電壓頻譜密度曲線進行積分計算,才能得到總噪聲值。事實上,我們必須對功率譜密度曲線進行積分計算。該曲線實際反映的是電壓或電流頻譜密度的平方(請記?。篜 = V2/R 且 P=I2R)。圖 2.6 顯示了對電壓頻譜密度曲線進行積分計算所得的奇怪結(jié)果。圖 2.7 顯示,您可將功率譜密度進行積分計算,再通過求結(jié)果的平方根將其轉(zhuǎn)換回電壓。請注意,我們由此可獲得合理結(jié)果。

圖 2.6:計算噪聲的不正確方法
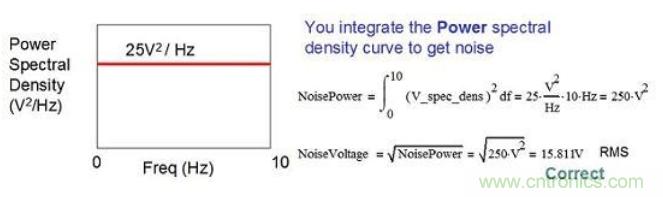
圖 2.7:計算噪聲的正確方法
通過對電壓與電流頻譜的功率譜密度曲線進行積分計算,我們可得到運算放大器模型信號源的 RMS 幅度(圖 2.3)。不過,頻譜密度曲線將分布在 1/f 區(qū)與帶低通濾波器的寬帶區(qū)(見圖 2.8)。如計算上述兩個區(qū)域的總噪聲,我們要采用微積分計算推導出的算式。再根據(jù) 部分所討論的處理非相關信號源的方法,對上述兩個計算的結(jié)果做和的平方根 (RSS) 運算,對應 部分中提到的非相關信號源。
首先,我們要對帶低通濾波器的寬帶區(qū)域進行積分計算。理想情況下,曲線的低通濾波器部分是一條縱向直線,我們稱之為磚墻式濾波器 (brick wall filter)。由于磚墻式濾波器情況下的曲線下方區(qū)域為矩形,因此這一區(qū)域的問題比較好解決,長乘寬即可。在實際情況下,我們不能實現(xiàn)磚墻式濾波器。不過,我們可用一組常量來將實際情況下的濾波器帶寬轉(zhuǎn)換為等效的磚墻式濾波器帶寬,以滿足噪聲計算的需要。圖 2.9 將理論磚墻式濾波器與一階、二階及三階濾波器進行了對比。
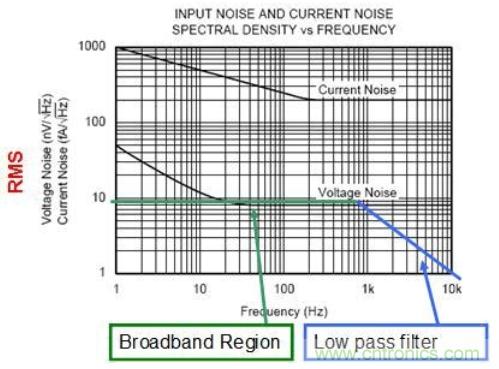
圖 2.8:帶濾波器的寬帶區(qū)
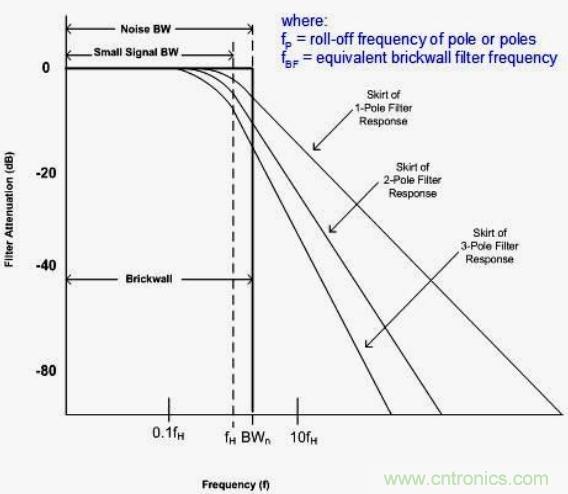
圖 2.9:磚墻式濾波器與實際濾波器相比較
我們可用方程式 2.2 用于轉(zhuǎn)換實際濾波器或做磚墻式濾波器等效。表 2.1 列出了各階濾波器的換算系數(shù) (Kn)。舉例來說,一階濾波器帶寬乘以 1.57 即為磚墻式濾波器帶寬。調(diào)節(jié)后的帶寬有時也稱作噪聲帶寬。請注意,換算系數(shù)隨著濾波器階數(shù)的提升將越來越接近于1。換言之,濾波器階數(shù)越高,就越接近于磚墻式濾波器。
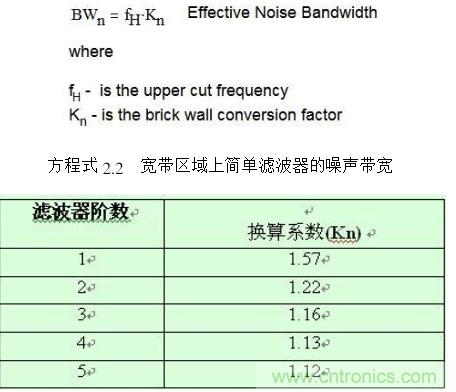
既然我們有了將實際濾波器轉(zhuǎn)換為磚墻式濾波器的算式,那么我們就能很方便地進行功率頻譜的積分運算了。請記住,功率的積分運算為電壓頻譜的平方。我們需將積分結(jié)果進行平方根運算轉(zhuǎn)換回電壓。方程式 2.3 即由此得出(見附錄 2.1)。因此,根據(jù)產(chǎn)品說明書中的數(shù)據(jù)套用方程式 2.2 、方程式 2.3便可計算出寬帶噪聲。
方程式 2.3:寬帶噪聲方程式
我們需記住,我們的目標是測定圖 2.3 中噪聲源 Vn 的幅度。該噪聲源包括寬帶噪聲與 1/f 噪聲。我們用方程式 2.2 與 2.3 可計算出寬帶噪聲?,F(xiàn)在我們應計算 1/f 噪聲,這就需求對噪聲頻率密度圖 1/f 區(qū)域的功率頻譜進行積分計算(如圖 2.10所示)。我們可用方程式 2.4 和 2.5 獲得有關積分結(jié)果。方程式 2.4 將 1/f 區(qū)的噪聲測量結(jié)果歸一化為 1Hz 時的噪聲。某些情況下,我們可從圖中直接讀出該數(shù)值,有時用方程式更方便求得(見圖 2.11)。方程式2.5用歸一化噪聲、上部噪聲帶寬與下部噪聲帶寬來計算 1/f 噪聲。附錄 2.2 給出了整個演算過程。
在考慮 1/f 噪聲時,我們必須選擇低頻截止點。這是因為 1/f 函數(shù)分母為零時無意義(即 1/0 無意義)。事實上,理論上 0 赫茲時噪聲趨近于無窮。但我們應當考慮到,頻率極低時,其相應的時間也非常長。舉例來說,0.1Hz 對應于 10 秒,而 0.001Hz則對應于 1000 秒。對極低的頻率而言,對應的時間有可能為數(shù)年(如 10nHz 對應于 3 年)。頻率間隔越大,積分計算所得的噪聲就越大。不過我們也要記住,極低頻噪聲檢測需要很長時間。我們在以后的文章中將更詳細地探討此問題。目前,我們暫且記住這一點,1/f 計算時通常用 0.1Hz 作為低頻截止點。
既然我們已得到了寬帶與 1/f 噪聲的幅度,現(xiàn)在就用 部分給出的無相關噪聲源算式來疊加噪聲源 (見如下方程式 2.6 與本系列文章的 部分中的方程式 1.8)。
工程師考慮分析方法時通常會擔心,1/f 噪聲與寬帶噪聲是否應在兩個不同的區(qū)域進行積分計算。換言之,他們認為,由于 1/f 噪聲與寬帶噪聲相加后會超出 1/f 區(qū)域,從而出現(xiàn)錯誤。實際上,1/f 區(qū)域與寬帶區(qū)域一樣,都涵蓋所有頻率。我們必須記住,當噪聲頻譜顯示在對數(shù)圖上,1/f 區(qū)在降至寬帶曲線以下后影響極小。兩條曲線結(jié)合明顯的 區(qū)域就在 1/f 半功率頻點處。在此區(qū)域中,我們看到兩區(qū)域結(jié)合部的情況與數(shù)學模型相同。圖 2.12 顯示了兩區(qū)實際重疊的情況,并給出了相應的幅度。
現(xiàn)在,我們已得到了將噪聲頻譜密度曲線轉(zhuǎn)換為噪聲源所需的全部方程式。請注意,現(xiàn)在我們已推算出了電壓噪聲所需的方程式,不過相同的方法也可運用于電流噪聲的計算。在本系列隨后的文章中,我們將討論用有關方程式來解決運算放大器電流的噪聲分析問題。
免責聲明:本文為轉(zhuǎn)載文章,轉(zhuǎn)載此文目的在于傳遞更多信息,版權(quán)歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權(quán)問題,請電話或者郵箱聯(lián)系小編進行侵刪。








